コンプリート！ (1-x^2)y''-2xy' 6y=0 power series solution 488473

We shall look for a power series solution around x o = 2;These issues are settled by the theory of power series and analytic functions 12 Power series and analytic functions A power series about a point x0 is an expression of the form X n=0 ∞ a n (x − x0) n = a 0 a1 (x − x0) a2 (x − x0) 2 (24) Following our previous discussion, we want to know whether this infinite sum indeedSolution 1 First assume y 2 =ux 2, and y 2 '=2uxu'x 2 and y 2 ''=u''x 2 4u'x2u Substituting into x 2 y''2xy'6y=0 we get x 2 (u''x 2 4u'x2u)2x(2uxu'x 2)6y=0 and simplifying by adding like terms we get u''x 4 6u'x 3 =0 We reduce the order by w=u' to get w'x 4 6wx 3 =0 Now dividing by wx 4 and rearranging, we get

Calameo Solution Techniques For Elementary Partial Differential Equations 2nd Constanda

(1-x^2)y''-2xy' 6y=0 power series solution

(1-x^2)y''-2xy' 6y=0 power series solution-C) express the solution satisfying y(0) = 1, y′(0) = −1 in terms of y1(b) 2xy′′ (3−x)y′ − y = 0 Solution (a) Write the differential equation in standard form y′′ − 1 2x y′ 1 4x y = 0 We have P(x) = − 1 2x and Q(x) = 1 4x, so x = 0 is a singular point Taking limits we get lim x→0 xP(x) = −1/2 and lim x→0 x2Q(x) = 0 Therefore x = 0

1a Engineering Mathematics Ppt Download

 By taking the derivative term by term, y'=sum_{n=1}^infty nc_nx^{n1} Now, let us look at the differential equation y'=xy by substituting the above power series in the equation, Rightarrow sum_{n=1}^infty nc_nx^{n1}=x cdot sum_{n=0}^\inftyc_nx^n by pulling the first term from the summation on the left, Rightarrow c_1sum_{n=2}^inftync_nx^{n1Find second solution to {eq}x^22xy"6y=0 {/eq} given that {eq}y1=x^2 {/eq} Solution of differential equation The given differential equation is a second order linear differential equationIe, a solution of the form (258) y(x) = X1 n=0 a n (x 2) n Our task is then is to determine the coe cients a n so that this y(x) indeed satis es (257) Now already the rst two coe cients are determined by the initial conditions To see this note (259) y(x) = P 1 n=0 a n (x 2) n = a

Answer to Solve 2xy''(x1)y'2y=0 by method of power series Get more out of your subscription* Access to over 60 million coursespecific study resourcesAnswer (1 of 4) Step 1 The trick is to make the change of (independent) variable t = ln x, to reduce the equation to a linear differential equation with constant coefficients, which presumably you already know how to solve Then x = e^t and dt/dx = 1/x If you are careful with the product ruleSolve The Differential Equation 1 X Y 2xy 6y 0 By Using The Series Solution Method Homeworklib Y 22y12xy=0, from which y 2 2 (x1)y1=0, from which y=1x±√ ( (x1) 21) by the quadratic formula or alternatively, y=1x±√ (x 22x) Either way, you can pick any value of one variable that makes sense in the expression, to get the corresponding value

 Let y be a polynomial solution of the differential equation ( 1 − x 2) y ″ − 2 x y ′ 6 y = 0 If y ( 1) = 2, then the value of the integral ∫ − 1 1 y 2 d x is First of all I can solve it by conventional method, which is long and provided this is a competitive exam question, the maximum time I can give is 2 − 3 minsMy Patreon page https//wwwpatreoncom/PolarPiFull Power Series method for solving Diff Eqs Playlist https//wwwyoutubecom/watch?v=L93PLTrMGYI&list=PLsTB 0 (x)y" b 1 (x)y' b 2 (x)y = 0 Then the equation has a general solution either of the form or of the form where c 1 and c 2 are roots of the indicial equation and A and B are arbitrary constants

Matematikcimehmetyavuz Files Wordpress Com

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

6C6 Find two independent power series solutions n anx to (1 − x 2 )y − 2xy 6y = 0 Determine their radius of convergence R To what extent is R predictable from the original ODE?Answer (1 of 5) The equation \displaystyle{ (1x^2)y'' 2xy' 2y = 0 }\qquad(1) Since we have no obvious way to find any particular solution of (1) so we should try to find its general solution in the form of a power series as follows \displaystyle{ y = C_0 C_1x C_2x^2 \dots C_nx^2Can anyone give me an advice that helps me to solve this kind of DE $$ x^2 \cdot y'' 2x \cdot y' 2y = 0 $$ knowing that $$ y_1=Ax{B \over x^2} $$ is a solution

Is There A Legendre Polynomial In This Differential Equation 1 X 2 Y 2xy 6y 0 Quora

4 A Solve The Differential Equation 1 X 2 Y 2xy L L 1 Y 0 Using Power Series Centered At 0 In Which Homeworklib

If possible finod 1 and 12) 2 Find a power series expansion about 0 for a general solution to the given differential equation (z 1)y', _ y 0, solve the differential equation (1 – x?)y" 2xy'6y=0 by using the series solution method solve the differential equation (1 – x?)y" 2xy'6y=0 by using the series solution methodMath 115 HW #11 Solutions 1 Show that the power series solution of the differential equation y0 −py = 0 is equivalent to the solution found using some other technique The basic idea to finding a series solution to a differential equation is to assume that we can write the solution as a power series in the form, y(x) = ∞ ∑ n=0an(x−x0)n (2) (2) y ( x) = ∑ n = 0 ∞ a n ( x − x 0) n and then try to determine what the an a n 's need to be

Calameo Solution Techniques For Elementary Partial Differential Equations 2nd Constanda

Paginapessoal Utfpr Edu Br

Get an answer for 'Find a general solution using power swries ((x^2)1)y'' 6xy' 6y =0' and find homework help for other Math questions at eNotesAnswer (1 of 2) x1/y =2 2xy3y=2 x=21/y = (2y1)/y 2(2y1)/y 3y = 2 4y2 — 3y^2 =2y QUADRATIC EQUATION 3y^2 6y 2 =0 3y^2 6y 2=0 a=3 b=6 c=2 y= 6{eq}(1 x^2)y'' 2xy' 2y=0, {/eq} into a Maclaurin series to get a recurrence relation for the coefficients of the solution series By selecting appropriately the first two coefficients we'll

Decomposition Of Ordinary Differential Equations Topic Of Research Paper In Physical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

Set m= n2 n2, then rewrite the first sum in terms of m, then replace m with n 1 level 2 SterlinMerlin Op 7y So then in the following summations i need to put them in terms of m as well?Given the equation $$ 2 x y{\left(x \right)} \frac{d}{d x} y{\left(x \right)} = 2 x^{3}$$ This differential equation has the form y' P(x)y = Q(x)(a) 4xy′′ 2y′ y = 0;

Part 4 Bronson Differential Equations Schaum Pdf Document

Science Marshall Edu

8113 Find two linearly independent power series solutions to the dif ferential equation y′′ 9y = 0, and determine the radius of convergence for each series Also, identify the general solution in terms of familiar elementary functionsHow to Solve a Differential Equation with Series (x 1)y'' xy' y = 0 with y(0) = 2, y'(0) = 6If you enjoyed this video please consider liking, sharing,Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 100% (1 rating)

Pages Mtu Edu

Second Solution For Reduction Of Order X 2 1 Y 2xy 2y X 2 1 Youtube

X 1 y′ 2 x 1 y = 0 Then P(x) = −3x x 1 is singular at x = −1 and Q(x) = 2 x1 is also singular at x = −1 If R is the radius of convergence of a series solution, then R > x0 −(−1) = 2 (b) Write the equation in standard form y′′ − 3 x2 1 y = 0 Then P(x) = 0 is not singular anywhere but Q(x) = −3 x2 1 is singular at x = ±i See the answer See the answer done loading (1x^2)y''2xy'2y=0 Find the power series solution in powers of x show the details Expert Answer Who are the experts? Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Ualberta Ca

Power Series Solution Of Differential Equation X 2 1 Y 6y 0 Youtube

Answer to Use power series to solve the initialvalue problem y''2xy'4y=0, y(0)=0, y'(0)=1 By signing up, you'll get thousands of stepbystep See below Assuming a power series solution like this y = a_0 a_1 x a_2 x^2 a_3 x^3 ldots = sum_0^oo a_n x^n implies y^' = sum_1^oo n a_n x^(n1) qquad qquad y^('')= sum_2^oo n (n1)a_n x^(n2) With this power series y''2xy'y = 0 implies underbrace(sum_2^oo n (n1)a_n x^(n2))_(=sum_0^oo (m2) (m1)a_(m2) x^(m)) 2x sum_1^oo n a_n x^(n1) sum_0^oo a_n x^n= 0 implies sum_0^oo (n2) (n1)a_(n2) x^n 2 sum_1^oo n a_n x^n sum_0^oo a_n x^n= 0 implies 2 a_2 sum_1^oo (n2) (n1Soo in the second summation for eaxaple I would have Sum from m=2 to inf of (mr2) * (mr3) * a_ (m2) * x m2r 1 Continue this thread

Calculus 9e Purcell Varberg Rigdon Solution

Assume Y Xy Y 0 Has A Power Series Solution And Determine The Coefficient An Stumbling Robot

Find the first five terms of the power series solution for xy′′ yln(1 − x)=0 (24) and determine a lower bound for its radius of convergence Solution First we determine the radius of convergence Write the equation in standard form y 2 x2 y=0 (39) Thus p= 2 x 1 2 x,6C7 If the recurrence relation for the an has three terms instead of just two, it isExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music

17 Differential Equations Page 335 336 6 X6 B Cn 2 2n 1 N 2 N 1 Cn 17 5 Power Series Solutions 17 31 Exercises 17 5 In Exercises 118 Use Power Course Hero

Solved Find The Power Series Solution Of The Differential Equation About An Ordinary Point X 0 1 X2y 2xy 2y 0 Why We Find Power Series Soluti Course Hero

Exercise 215 For the equation \(x^2 y'' x y' = 0\text{,}\) find two solutions, show that they are linearly independent and find the general solution Hint Try \(y = x^r\text{}\) Equations of the form \(a x^2 y'' b x y' c y = 0\) are called Euler's equations or Cauchy–Euler equations They are solved by trying \(y=x^r\) and solvingODEs Find the first four terms of the power series solution to the IVP y"2y'y=x, y(0)=0, y'(0)=1 To check our answer, we find the solution using th2xy9x^2 (2yx^21) (dy)/ (dx)=0, y (0)=3 \square!

Power Series Solution For Y 2y Y X Y 0 0 Y 0 1 Youtube

Solved Find Two Power Series Solutions Of The Given Chegg Com

9 Find general solution of the following di erential equations given a known solution y 1 (i) (T) x(1 0x)y00 2(1 2x)y 2y= 0 y 1 = 1=x (ii) (1 2x)y00 2xy0 2y= 0 y 1 = x Solution (i) Here y 1 = 1=x Substitute y = u(x)=xto get (1 x)u00 2u0= 0 Thus, u0= 1=(1 x)2 and u= 1=(1 x) Hence, y 2 = 1=(x(1 x)) and the general solution is y= a=x b=(x The solution is y=c_0 cosxc_1 sinx Let us look at some details Let y=sum_{n=0}^inftyc_nx^n, where c_n is to be determined By taking derivatives, y'=sum_{n=1}^inftync_nx^{n1} Rightarrow y''=sum_{n=2}^inftyn(n1)c_nx^{n2} We can rewrite y''y=0 as sum_{n=2}^inftyn(n1)c_nx^{n2}sum_{n=0}^inftyc_nx^n=0 by shifting the indices of the first summation by 2, Rightarrow sum_{n=0}^infty(n2)(n1 #(k3)(k2)a_(k3)(k1)a_k=0# for #k = 0,1,2,3, cdots# This infinite recurrence equation needs the a priori definition of #a_0, a_1# which can

Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular

People Uncw Edu

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Nxn−1 6C2 Find two independent power series solutions P a nxn to y′′ −4y= 0, by obtaining a recursion formula for the a n 6C3 For the ODE y′′ 2xy′ 2y= 0, a) find two independent series solutions y1 and y2;5 Find a power series solution about x = 0 of the differential equation y′′ y = 0 6 Find a power series solution about x = 0 of the differential equation y′′−4y = 0 7 Find the recurrence relation for the terms in the power series solution about x = 0 of the differential equation y′′ xy = 0 8

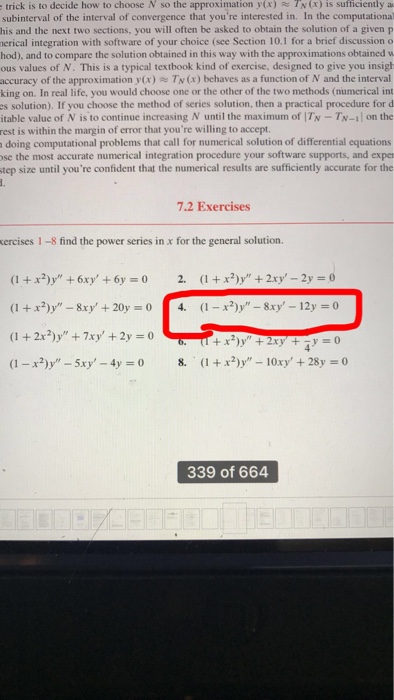
Solved Find The Power Series In X For The General Solution Chegg Com

Iitg Ernet In

B) determine their radius of convergence;

Solve The Differential Equation 1 X Y 2xy 6y 0 By Using The Series Solution Method Homeworklib

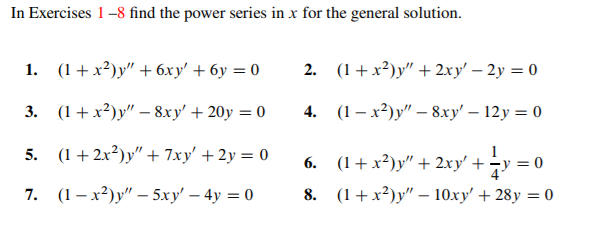
Solved In Exercises 1 8 Find The Power Series In X For The Chegg Com

Power Series Solution 1 X 2 Y 4xy 6y 0 Homeworklib

Solve The Differential Equation 1 X Y 2xy 6y 0 By Using The Series Solution Method Homeworklib

Math Utep Edu

Solved In Problems 1 14 For Each Differential Equation Chegg Com

How To Solve This Differential Equation Math 1 X 2 Y 6xy 4y 0 R T Math Quora

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 12y 0 Stumbling Robot

Solved Solve The Differential Equation 1 X2 Y 2xy 6y 0 Chegg Com

Chapter 1

Math Wisc Edu

Legendre Differential Equation Of Order Two 1 Chegg Com

Tau Ac Il

Introduction To Ordinary Differential Equations

Power Series Solution Of Differential Equation X 2 1 Y 6y 0 Youtube

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

Matematikcimehmetyavuz Files Wordpress Com

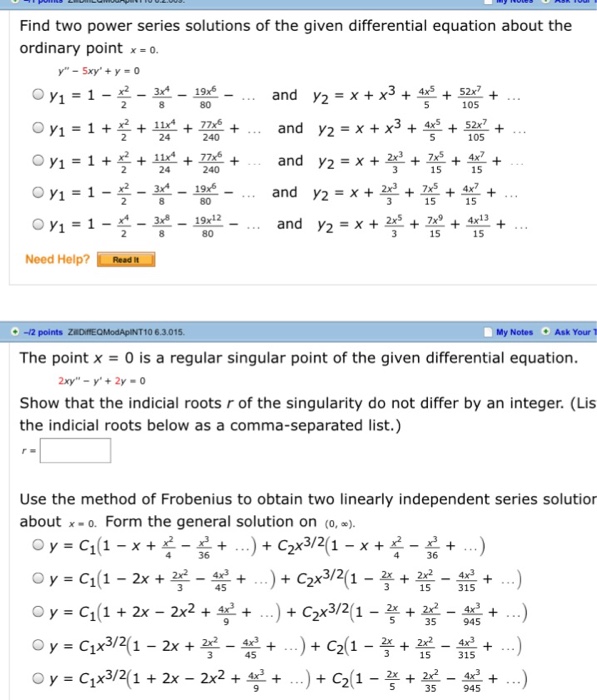
Find Two Power Series Solutions Of The Given Differential Equatio

Php Scripts Psu Edu

Thomas Calculus 12th Edition Thomas Solutions Manual

1a Engineering Mathematics Ppt Download

Find A Series Solution About The Point X 0 Of 1 X 2 Y 2xy 2y 0 Youtube

What Is The Solution Of The Differential Equation X 2 1 Y 2xy 2y 0 And What Type Of Differential Equation It This Quora

4 A Solve The Differential Equation 1 X 2 Y 2xy L L 1 Y 0 Using Power Series Centered At 0 In Which Homeworklib

Matematikcimehmetyavuz Files Wordpress Com

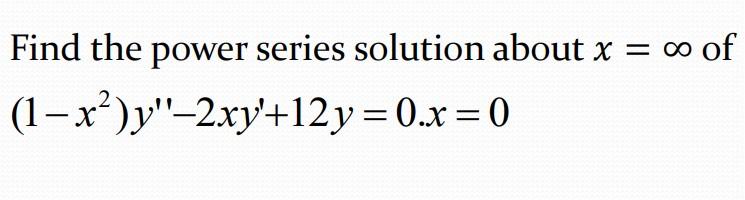
Answered Find The Power Series Solution About X Bartleby

Exact Equations Example 3 Video Khan Academy

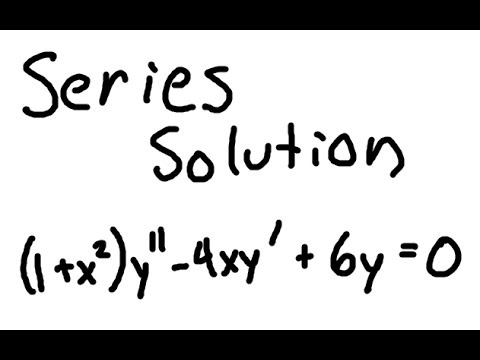
Series Solution Differential Equations Example 2 Youtube

Math Upenn Edu

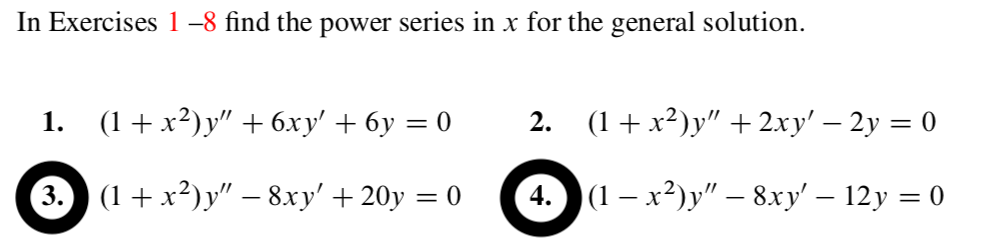
Solved In Exercises 1 8 Find The Power Series In X For The Chegg Com

Assignment 1

Uwyo Edu

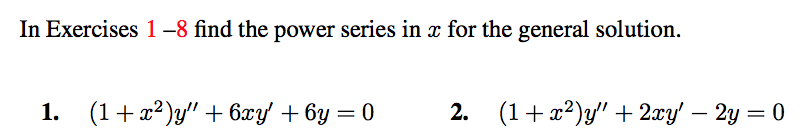
Solved In Exercises 1 8 Find The Power Series In X For The Chegg Com

Is There A Legendre Polynomial In This Differential Equation 1 X 2 Y 2xy 6y 0 Quora

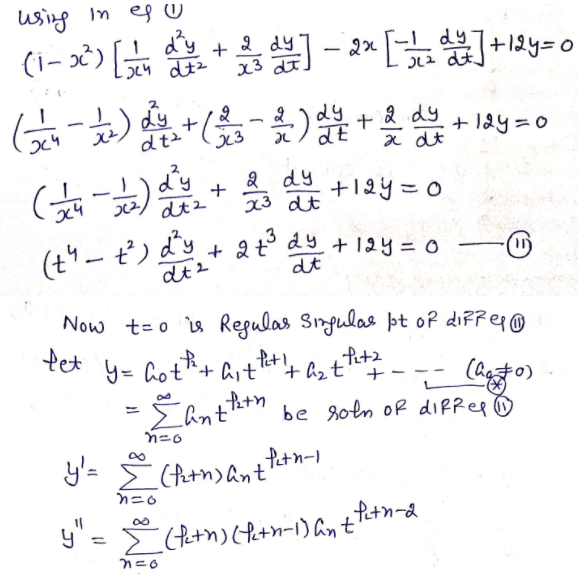
Answered Find The Power Series Solution About X Bartleby

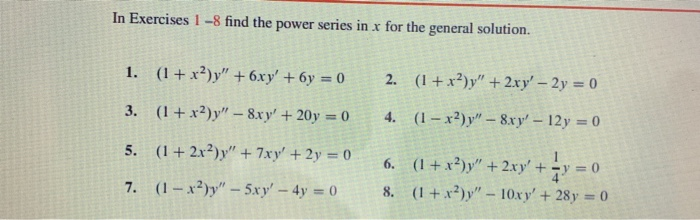
Solved In Exercises 1 8 Find The Power Series In X For The Chegg Com

Mat3110 19 Tutorial Sheet 1 Power Series Euler And Systems Pdf Eigenvalues And Eigenvectors Differential Equations

Assignment 1

Polynomial Solution Of The Equation 1 X 2 Y 2xy 6y 0 Mathematics Stack Exchange

People Whitman Edu

Calculus 9e Purcell Varberg Rigdon Solution

Ad Eng Math 6 8 15 Pages 51 100 Flip Pdf Download Fliphtml5

3 Consider The Following Differential Equation 0o And A Series Solution To The Differential Equation Of The Form A 34 Homeworklib

Math Upenn Edu

What Is The Solution To The Differential Equation Math 1 X 2 Y 2xy 2y 0 Math Quora

Pdf Advanced Engineering Mathematics Solutions Manual Ahmed Shaghasi Academia Edu

Solved Problems 7 18 Find Two Power Series Solutions Of The In Differential Equation About The Ordinary Point R 0 Given 7 7 Xy 0 8 Y Xly

Faculty Uca Edu

Power Series Solutions Of Differential Equations Ex 2 Youtube

Solved In Exercises 1 8 Find The Power Series In X For The Chegg Com

Power Series Solution 1 X 2 Y 4xy 6y 0 Homeworklib

1a Engineering Mathematics Ppt Download

Www2 Math Binghamton Edu

Site Iugaza Edu Ps

De Pdf Ordinary Differential Equation Equations

Faculty Math Illinois Edu

Pub Math Leidenuniv Nl

Solved 1 Find Two Linearly Independent Power Series Chegg Com

Iitg Ac In

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot

1

Frobenius Series Method Pdf Equations Recurrence Relation

Power Series Solution 1 X 2 Y 4xy 6y 0 Homeworklib

Canvas Eee Uci Edu

Solucionarioecuacionesdiferencialesdenniszill7aedicion P

Is There A Legendre Polynomial In This Differential Equation 1 X 2 Y 2xy 6y 0 Quora

4 A Solve The Differential Equation 1 X 2 Y 2xy L L 1 Y 0 Using Power Series Centered At 0 In Which Homeworklib

Macs Citadel Edu

Users Metu Edu Tr

Power Series Solution Of A Differential Equation

Power Series Solution To Y 2xy 0 Mathematics Stack Exchange

Matematikcimehmetyavuz Files Wordpress Com

Solve The Differential Equation 1 X Y 2xy 6y 0 By Using The Series Solution Method Homeworklib

Solved Consider The Second Order Equation Y 2ry 6y 0 What Does It Mean To Say That To 0 Is A Ordinary Point Of 1 2 B Find The Recurrence Relation

2nd Order Homogeneous Differential Equations Pdf Document

6 1 22 Find Power Series Solutions Of X 2 1 Y 6y 0 De Youtube